Equivariance Discovery by Learned Parameter-Sharing

Raymond A. Yeh¹   Yuan-Ting Hu   Mark Hasegawa-Johnson   Alexander G. Schwing  

Toyota Technological Institute at Chicago¹   University of Illinois Urbana-Champaign  

Abstract

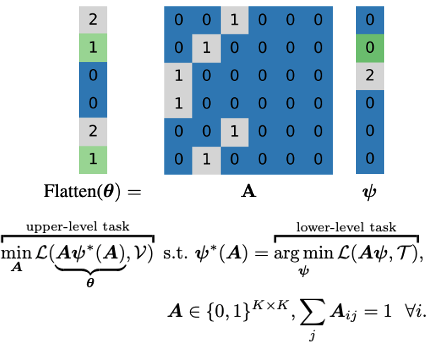
Designing equivariance as an inductive bias into deep-nets has been a prominent approach to build effective models, e.g., a convolutional neural network incorporates translation equivariance. However, incorporating these inductive biases requires knowledge about the equivariance properties of the data, which may not be available, e.g., when encountering a new domain. To address this, we study how to discover interpretable equivariances from data. Specifically, we study this discovery process when using an optimization problem over a model’s parameter-sharing schemes. Also, we propose to use partition distance to empirically quantify the accuracy of recovered equivariance. We analyze this approach for Gaussian data and provide a bound on the mean squared gap between the studied discovery scheme and the oracle scheme. Empirically, we show that this approach recovers known equivariances, such as permutations and shifts, on sum of numbers and spatially-invariant data.

Materials

[Paper]

[Poster]

Code

[GitHub]

Presentation

Citation

@inproceedings{YehAISTATS2022,
               author = {R.~A. Yeh and Y.-T. Hu and M. Hasegawa-Johnson and A.~G. Schwing},
               title = {Equivariance Discovery by Learned Parameter-Sharing},
               booktitle = {Proc. AISTATS},
               year = {2022},
}